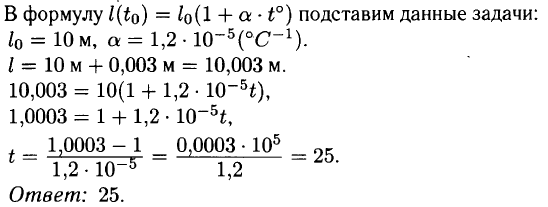ЕГЭ по математике Профиль. Задание 8: Уметь строить и исследовать простейшие математические модели. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
ЕГЭ Профиль. Задание № 8
АЛГОРИТМ ВЫПОЛНЕНИЯ
Задание № 8 определяет умение строить и исследовать простейшие математические модели, решать текстовые задачи на сложные проценты, использование арифметической и геометрической прогрессии, различные виды движения, вычисление работы.
Задание состоит из текстовой задачи с описанием различных жизненных ситуаций. Как правило, решение требует составления уравнения или системы уравнении. В ответе следует записать целое число или конечную десятичную дробь.
План выполнения:
- Внимательно прочитайте условие задачи.
- Сделайте краткую запись.
- Составьте выражение, уравнение или систему уравнений.
- Выполните решение на черновике. При получении двух корней в уравнении оставьте корень, подходящий по смыслу к условию задачи. Ответьте на вопрос задачи.
- Запишите полученное число в поле ответа КИМ и бланк ответов N 1.
При подготовке необходимо повторить правила решения задач с использованием следующих величин и понятий:
- Сложные проценты, где процент вычисляется несколько раз. При подготовке необходимо повторить понятие процента от числа и правила нахождения процента от числа, числа по его проценту, процента по числу.
- Концентрация смесей и сплавов. Концентрация — процентное отношение чистого вещества к смеси (сплаву, раствору). Такие задачи решаются с помощью процентов или пропорции.
- Движение по прямой. Из курса физики следует повторить формулы для нахождения скорости, закон сложения скоростей.
- Движение по окружности. Такие задачи в большинстве случаев решаются составлением уравнений или систем уравнений.
- Движение по течению и против течения. Подобные задачи также решаются составлением уравнения или системы уравнений.
- Работа и совместная работа. Для решения применяются уравнения или системы уравнений.
- Арифметическая и геометрическая прогрессии. При подготовке необходимо повторить определения прогрессий, формулы для вычисления отдельных членов арифметической и геометрической прогрессии, суммы членов.
Задачи с ответами и решениями:
Задача № 8 (1). В октябре цена на яблоки была снижена на 10% по отношению к цене в сентябре. В ноябре октябрьская цена повысилась на 10%. Сколько процентов составляет ноябрьская цена по отношению к сентябрьской?
Решение: Пусть х — цена на яблоки в сентябре, тогда в октябре цена составила 90% от сентябрьской и равна 0,9х. После повышения в ноябре на 10% цена составила 110% от октябрьской и равна 1,1 • (0,9х) = 0,99х. Значит, в ноябре цена составила 0,99 от цены в сентябре, то есть 99%.
Ответ: 99.
ПРИМЕЧАНИЕ: Процент означает сотую часть чего–либо. 1 % от числа означает 0,01 этого числа. В ходе решения удобно сразу переводить проценты в десятичные дроби.
Часто учащиеся пишут в ответе 0, объясняя это тем, что если цена была снижена на 10%, а затем повысилась на 10%, то конечная цена не изменилась.
Задача № 8 (2). Имеется кусок сплава меди с оловом общей массой 12 кг, содержащий 45% меди. Сколько чистого олова надо добавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди?
Решение: Пусть х кг олова надо добавить к сплаву. Так как процентное содержание меди в сплаве равно 45%, масса меди в первоначальном сплаве m = 0,45 • 12 = 5,4 (кг). Тогда 12 + х — масса нового сплава. Поскольку масса меди в первоначальном сплаве равна 5,4 кг, то 5,4/(12+х) – концентрация меди в новом сплаве. По условию 5,4/(12+х) = 0,4. Решая уравнение, получаем: х = 1,5 (кг)
Ответ: 1,5.
ПРИМЕЧАНИЕ: Концентрация меди в новом сплаве равна отношению массы меди к общей массе нового сплава.
Задача № 8 (3). В сосуд, содержащий 4 л 14%–ного водного раствора некоторого вещества, добавили 6 л воды. Сколько процентов составляет концентрация получившегося раствора?
Решение: Концентрация раствора равна р = Vв–ва/Vр–ра • 100%. Объём вещества в исходном растворе равен 0,14 • 4 = 0,56 (л). При добавлении 6 л воды общий объём раствора стал 10 л, а объём растворённого вещества остался прежним. Таким образом, концентрация полученного раствора равна 0,56/10 • 100% = 5,6%.
Ответ: 5,6.
ПРИМЕЧАНИЕ: Концентрация раствора равна отношению массы растворённого вещества к массе раствора, а также отношению их объёмов.
При решении задач на смешивание удобно пользоваться формулой m1с2 + m2с2 = (m1 + m2)с3, где m1, m2 — массы смешиваемых растворов, с1, с2, с3 — концентрации растворов до и после смешивания.
Задача № 8 (4). Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 12 км. Через сколько часов мотоциклисты поравняются в первый раз, если скорость одного из них на 3 км/ч больше скорости другого?
Решение: Пусть v км/ч — скорость первого мотоциклиста, тогда скорость второго мотоциклиста равна v + 3 км/ч.
Пусть первый раз мотоциклисты поравняются через t ч. Для того чтобы мотоциклисты поравнялись, более быстрый должен преодолеть изначально разделяющее их расстояние, равное половине длины трассы. Поэтому (v + 3)t – vt = 6, отсюда t = 2. Таким образом, мотоциклисты поравняются через 2 ч.
Ответ: 2.
ПРИМЕЧАНИЕ: Движение по окружности определяется теми же формулами, что и движение по прямой: S = vt; v =S/t; t = S/v.
Задача № (5). Бригада маляров красит забор длиной 360 м, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 80 м забора. Определите, сколько дней бригада маляров красила весь забор.
Решение: Пусть бригада в первый день покрасила а1 м забора, во второй — а2, … , в последний — аn м забора. Тогда а1 + аn = 80 (м), а за n дней было покрашено Sn = (а1 + аn)/2 • n = 80n/2 = 40n (м). Поскольку всего было покрашено 360 м забора, имеем: 40n = 360; n = 9. Таким образом, бригада красила забор в течение 9 дней.
Ответ: 9.
ПРИМЕЧАНИЕ: Поскольку ежедневно бригада увеличивала норму на а м забора, следует использовать формулу суммы арифметической прогрессии.
Тренировочные задания с самопроверкой
№ 8.1. Из двух городов А и В, расстояние между которыми равно 360 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 135 км от города В. За сколько часов автомобиль, выехавший из города А, доедет до города В?
№ 8.2. Первые два часа теплоход шёл со скоростью 20 км/ч, следующий час – со скоростью 30 км/ч, а затем четыре часа – со скоростью 28 км/ч. Найдите среднюю скорость теплохода на протяжении всего пути. Ответ дайте в км/ч.
№ 8.3. Скоростной поезд, двигаясь равномерно со скоростью 150 км/ч, проезжает мимо семафора за 15 секунд. Найдите длину поезда в метрах.
№ 8.4. В помощь насосу, перекачивающему 200 литров воды за 4 минуты, подключили второй насос, который перекачивает тот же объём воды за 6 минут. За сколько минут два эти насоса перекачают 5000 литров воды, работая вместе?
№ 8.5. В мае в магазине продали товаров на 325000 рублей. В июне сумма продаж возросла на 12%, а в июле – снизилась на 10% по сравнению с июнем. На сколько рублей продал магазин товаров в июле?
Вы смотрели: ЕГЭ по математике Профиль. Задание 8: Уметь строить и исследовать простейшие математические модели. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».