Рубрика: Ответы

ЕГЭ Решение задач по физике. Механика 11-20ЕГЭ Решение задач по физике. Механика 11-20

24.06.201924.06.2019 | Нет комментариев | 07:39

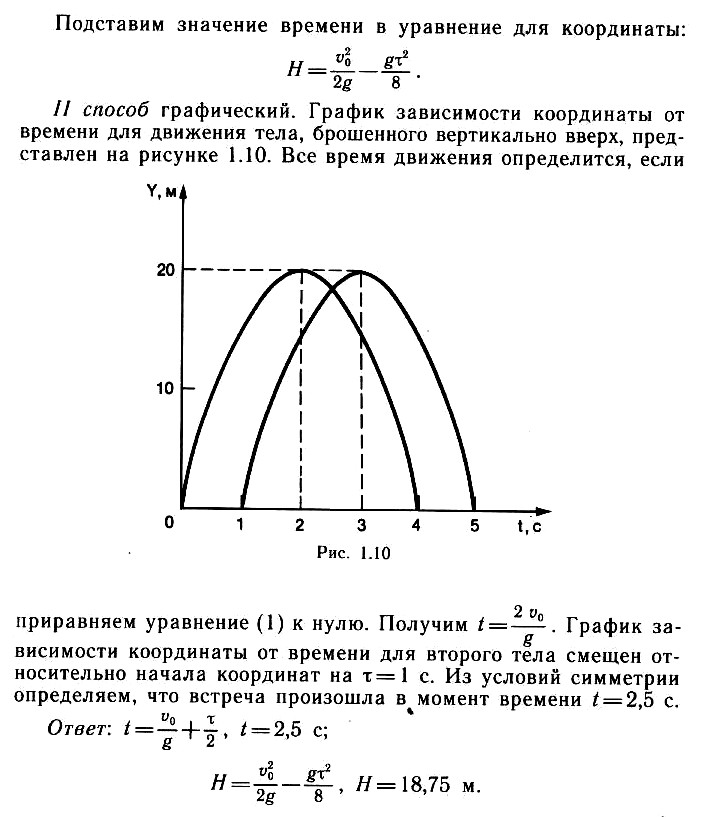
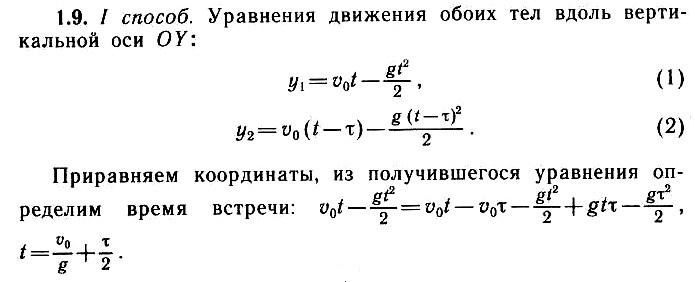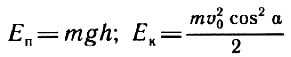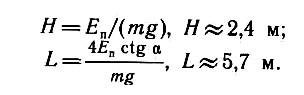ЕГЭ Решение задач по физике. Глава 1. МЕХАНИКА (кинематика, динамика, статика, колебания и волны).

Задачи ЕГЭ по физике М11 — М20 с указаниями, подсказками, ответами и решениями (ГДЗ по ЕГЭ). Материал для подготовки к ЕГЭ по физике может быть использован репетиторами, учителями и самими учащимися.

Вернуться к Списку заданий тренинга по физике.

 

Задачи по физике.
Механика 11-20

Задача 1.11. Тело массой m = 400 г брошено с некоторой высоты по направлению к земле под углом α = 30° к горизонту. Начальная скорость тела ʋ0 = 20 м/с. Определите, через сколько времени скорость тела будет направлена под углом β = 60° к горизонту. Определите изменение потенциальной энергии тела за это время. Ускорение свободного падения g ≈ 10 м/с2.

Указания (подсказка)
Покажите на рисунке направление горизонтальной, вертикальной и полной скоростей тела в начальный момент времени и в искомый момент времени. Учтите, что горизонтальная составляющая скорости не изменяется, а вертикальная увеличивается с течением времени. Вспомните определение тангенса угла и из треугольника скоростей получите уравнение для времени. Изменение потенциальной энергии определите из закона сохранения энергии или как работу силы тяжести за указанный промежуток времени.
Решение и ответ

 

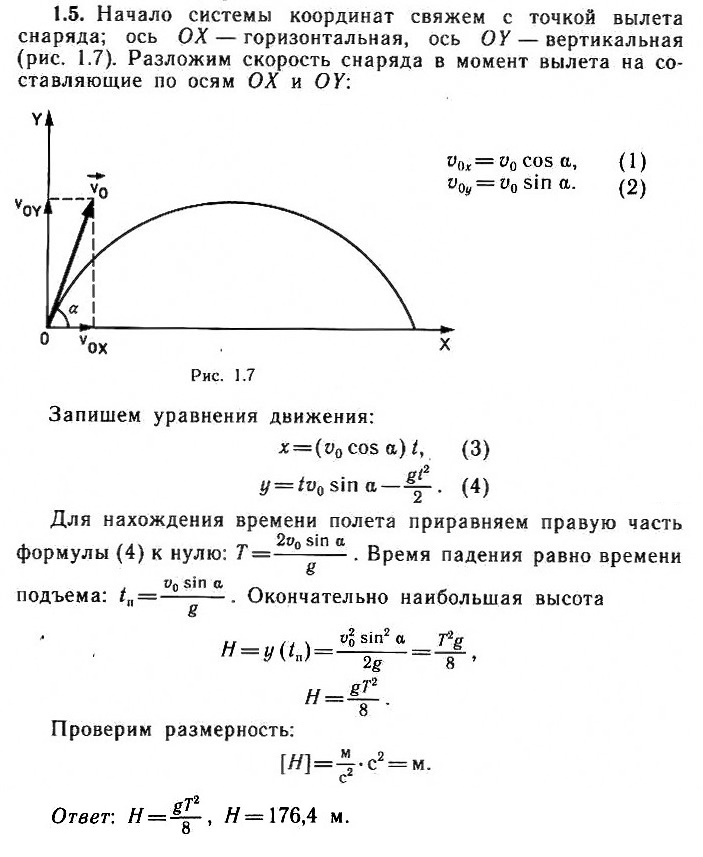
Задача 1.12. Тело массой m = 0,5 кг брошено со скоростью ʋ0 = 20 м/с под углом α = 30° к горизонту. Определите наибольшую высоту полета н изменение импульса за время полета. Сопротивлением воздуха можно пренебречь. Примите g ≈ 10 м/с2.

Указания (подсказка)
Наибольшую высоту подъема определите или из уравнения движения, или из закона сохранения энергии (см. задачу 1.10). Изменение импульса определите как разность векторов конечного и начального импульсов. Внимание! Не забывайте о векторном характере импульса. Можно воспользоваться вторым законом Ньютона. Изменение импульса системы равно импульсу внешней силы. Этой силой является сила тяжести.
Решение и ответ

 

Задача 1.13. Катер пересекает реку шириной l = 360 м. Скорость течения ʋ = 2 м/с. Рулевой держит курс перпендикулярно течению. Двигатель обеспечивает постоянное ускорение а = 0,1 м/с2. Начальная скорость катера равна нулю. Определите, через сколько времени катер пересечет реку. На какое расстояние он будет снесен течением?

Указания (подсказка)
Катер участвует в двух движениях: по течению реки он движется равномерно, а перпендикулярно течению относительно воды его движение равноускоренное.
Решение и ответ

 

Задача 1.14. Из окна вагона поезда, движущегося по горизонтальной дороге со скоростью ʋ = 54 км/ч, бросают в горизонтальном направлении предмет. Предмет падает на землю на расстоянии s = 12,1 м от места, над которым он находился в момент бросания. Определите скорость ʋ0 предмета относительно вагона сразу после бросания, если она была направлена перпендикулярно скорости движения поезда. Высота окна над поверхностью земли H = 2,5 м. Сопротивлением воздуха можно пренебречь.

Указания (подсказка)
Необходимо воспользоваться принципом относительности движения, рассматривая движение одного тела относительно другого или относительно Земли. Вспомните правило сложения скоростей: скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости этой подвижной системы относительно неподвижной. Помните о векторном характере скоростей. Если вам трудно запомнить такие «сложные» закономерности, вспомните простое правило сложения скоростей для лодки, переплывающей реку: течение ее сносит вдоль берега, а рулевой стремится переправиться на противоположный берег. И тогда любая задача, связанная с относительностью движения, будет вами решена.
Решение и ответ

 

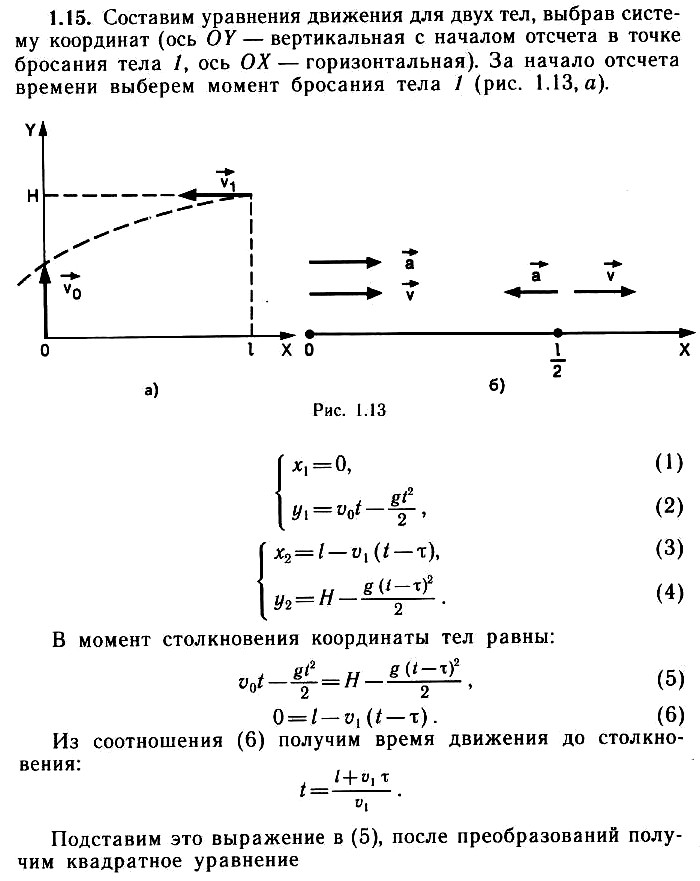
Задача 1.15. Тело 1 бросают вертикально вверх с начальной скоростью ʋ0 = 30 м/с. Тело 2, находящееся на высоте Н = 40 м по вертикали и на расстоянии l = 20 м по горизонтали от точки бросания тела 1, бросают горизонтально со скоростью ʋ1 =20 м/с. Определите, с каким запаздыванием или опережением т надо бросить тело 2, чтобы тела столкнулись в полете. Ускорение свободного падения g ≈ 10 м/с2.

Указания (подсказка)
Необходимо воспользоваться принципом относительности движения, рассматривая движение одного тела относительно другого или относительно Земли. Вспомните правило сложения скоростей: скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости этой подвижной системы относительно неподвижной. Помните о векторном характере скоростей. Если вам трудно запомнить такие «сложные» закономерности, вспомните простое правило сложения скоростей для лодки, переплывающей реку: течение ее сносит вдоль берега, а рулевой стремится переправиться на противоположный берег.
Решение и ответ

 

Задача 1.16. Человек начинает подниматься по движущемуся вверх эскалатору метро с ускорением а = 0,21 м/с2. Добежав до середины эскалатора, он останавливается, поворачивает и начинает спускаться вниз с тем же ускорением. Определите, сколько времени человек находится на эскалаторе. Длина эскалатора l = 100 м, а скорость его движения ʋ = 2 м/с.

Указания (подсказка)
Смотрите указание к задаче 1.14 
Решение и ответ

 

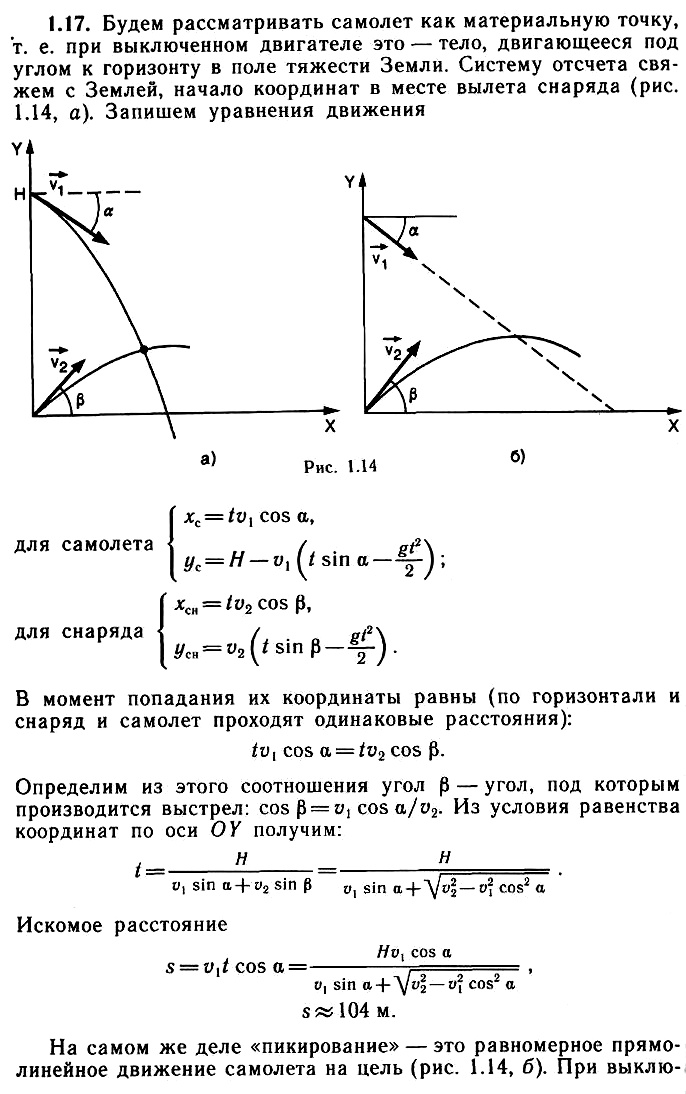
Задача 1.17. Самолет, пролетая над зенитной батареей на высоте H = 1 км, начинает пикировать с выключенным двигателем на цель со скоростью ʋ1 = 540 км/ч, направленной под углом а = 60° к горизонту. Самолет сбивают выстрелом из орудия, произведенным в тот момент времени, когда он находился над батареей. Определите, на каком расстоянии от батареи, считая по горизонтальному направлению, снаряд попал в сaмолет. Скорость снаряда при вылете из ствола орудия ʋ2 = 600 м/с. Сопротивлением воздуха можно пренебречь.

Указания (подсказка)
Смотрите указание к задаче 1.14. Выберите систему отсчета, связанную с Землей, и составьте уравнения движения для снаряда и самолета. Равенство соответствующих координат и означает момент столкновения.
Решение и ответ

 

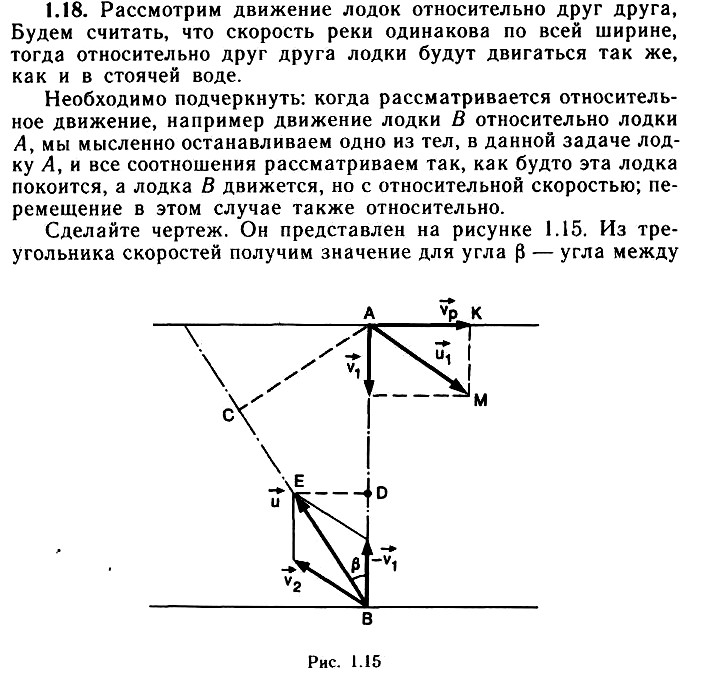
Задача 1.18. Две лодки переплывают реку, отправляясь одновременно из пунктов A и В, расположенных на противоположных берегах реки против друг друга. Скорость течения реки ʋp = 20 м/мин, ширина реки l = 200 м. Скорости лодок относительно воды равны ʋ1 = 15 м/мин, ʋ2 = 20 м/мин. Первая лодка начала движение перпендикулярно течению, а вторая держит курс под углом α = 150° к скорости течения реки. Определите, на каком расстоянии от пункта А будет находиться первая лодка, когда расстояние между лодками будет наименьшим.

Указания (подсказка)
После построения векторов скоростей учтите, что наименьшее расстояние между лодками будет определяться перпендикуляром из точки А на направление относительной скорости для лодки, выходящей из пункта В. Для того чтобы это понять, мысленно остановите лодку в пункте А, тогда вторая лодка должна двигаться в направлении относительной скорости, это ее перемещение, а наименьшее расстояние есть перпендикуляр, опущенный из точки на выбранное направление!
Решение и ответ

 

Задача 1.19. Лодочник отплывает из пункта А, держа курс перпендикулярно берегу. Скорость течения реки ʋp = 2 м/с, ее ширина h = 144 м. Лодка в течение времени t1 движется равноускоренно с ускорением а = 1 м/с2, а затем в течение промежутка времени t2 движется равномерно и, наконец, в течение промежутка времени t3 – равнозамедленно с тем же ускорением а. Определите промежутки времени t1 и t2, если известно, что лодка пришла в пункт В, расположенный на противоположном берегу реки на расстоянии l = 80 м вниз по течению. Постройте траекторию движения лодки в системе координат (XOY), связанной с берегом.

Указания (подсказка)
Выберите оси координат по течению реки и в перпендикулярном направлении. Запишите уравнения движения по обеим осям. Решите полученную систему.
Решение и ответ

 

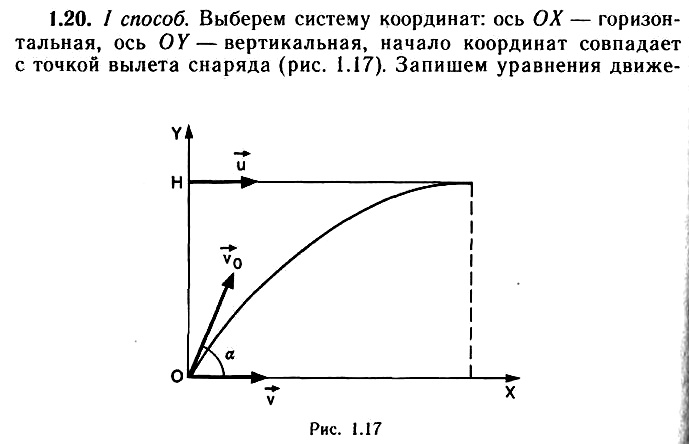
Задача 1.20. Из танка, движущегося со скоростью ʋ = 70 км/ч, стреляют по горизонтально летящему на высоте Н = 6 км самолету. Скорость самолета ʋ = 790 км/ч, а ее направление совпадает с направлением движения танка. Определите угол вылета α снаряда относительно горизонта. Известно, что в момент выстрела самолет находился над танком, а снаряд попал в самолет в высшей точке траектории.

Указания (подсказка)
Выберите систему отсчета, связанную с Землей, и составьте уравнения движения для снаряда и самолета. Равенство соответствующих координат и означает момент столкновения.
Решение и ответ

 

Вы смотрели «ЕГЭ Решение задач по физике. Механика 11-20». Задачи ЕГЭ по физике с указаниями, подсказками, ответами и решениями (ГДЗ по ЕГЭ). Материал для подготовки к ЕГЭ по физике.

Вернуться к Списку заданий тренинга по физике.

Читать далееЧитать далее

ЕГЭ Решение задач по физике. Механика 01-10ЕГЭ Решение задач по физике. Механика 01-10

23.06.201923.06.2019 | Нет комментариев | 18:46

ЕГЭ Решение задач по физике. Глава 1. МЕХАНИКА (кинематика, динамика, статика, колебания и волны). Задачи ЕГЭ по физике М01 — М10 с указаниями, подсказками, ответами и решениями (ГДЗ для ЕГЭ). Материал для подготовки к ЕГЭ по физике может быть использован репетиторами, учителями и самими учащимися.

Вернуться к Списку заданий тренинга по физике.

Задачи по физике. Механика 01-10

Задача 1.1.  Движение материальной точки задано уравнением x = At+ Bt2, где А = 2 м/с, В = –2 м/с2. Определите ускорение движения точки н путь, пройденный ею до остановки. Постройте графики зависимости от времени ускорения, скорости и координаты.

Указания (подсказка)
При решении этой задачи обычно возникают математические трудности. Вспомните, что скорость определяется как производная по времени от функции координаты, а ускорение – как производная по времени от функции скорости. Но вы забыли это определение или забыли, как надо взять производные. Что делать? Запишите основные два уравнения:
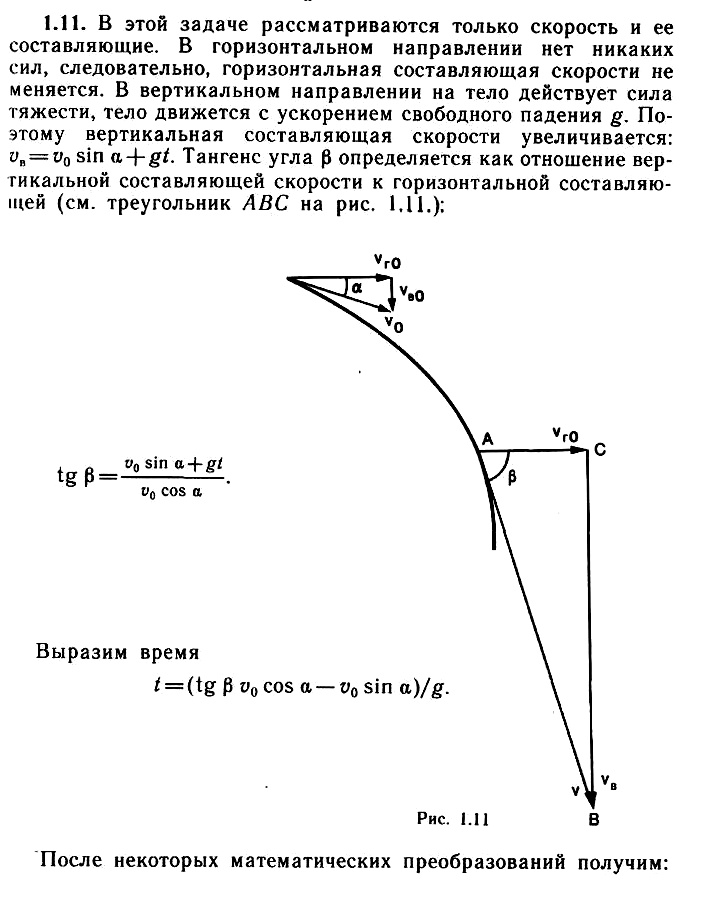
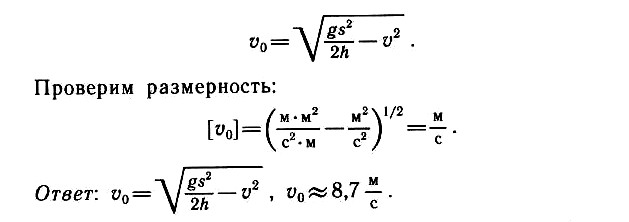
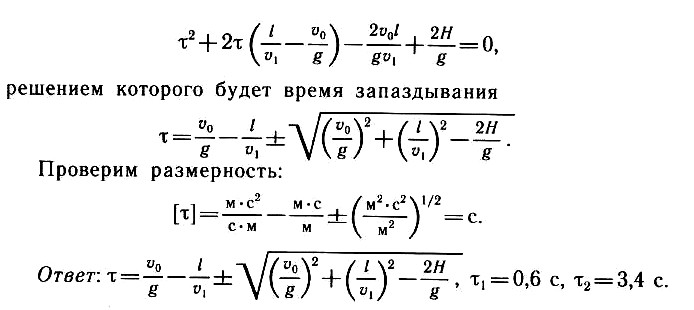
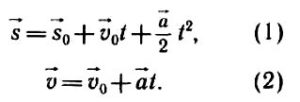В момент времени, когда скорость равна нулю, s и есть пройденный путь.
Решение и ответ

Задача 1.2. На рисунке дан график зависимости ускорения от времени при прямолинейном движении материальной точки. Постройте графики зависимости скорости от времени для этого движения. Определите путь, пройденный точкой за все время движения. Рассмотрите случаи, когда: 1) начальная скорость равна нулю; 2) начальная скорость ʋ0 = 2 м/с; 3) начальная скорость ʋ0 = – 1 м/с. Постройте также графики зависимости координаты от времени; начальная координата равна нулю (х0 = 0).

задача 1.2

задача 1.2

Указания (подсказка)

Внимательно изучите график. На промежутке 0 ≤ t ≤ 4 с ускорение постоянно и положительно; следовательно, его направление совпадает с направлением выбранной системы координат, площадь под графиком определяет приращение скорости. Для промежутка времени 4 с ≤ t ≤ 8 с движение равнозамедленное ускорение отрицательно. Составьте уравнения зависимости скорости и координаты от времени, руководствуясь соотношениями (1) и (2). Не забудьте при этом о выборе начала отсчета времени. Вспомните также, что путь определяется площадью под графиком зависимости скорости от времени; суммируйте все площади и над осью времени, и под осью времени.

Решение и ответ

Задача 1.3. Две материальные точки движутся прямолинейно.  Графики зависимости скорости от времени приведены на рисунке; ломаная ОАВС – для первой точки, ODC – для второй. Опишите характер движения точек. Постройте графики зависимости ускорения и координаты от времени.

задача 1.3

задача 1.3

Указания (подсказка)
Воспользуйтесь указанием к задаче 1.2.
Решение и ответ
Задача 1.4. Из окна вагона, движущегося по горизонтальному пути со скоростью ʋ = 54 км/ч, выпал предмет. Окно расположено на высоте h = 2,5 м от поверхности земли. Определите расстояние от места, где предмет выпал из окна, до места его падения на землю.

Указания (подсказка)
 Выберите систему координат, взяв за начало отсчета точку бросания; ось ОХ – горизонтально направленную вдоль движения вагона, ось OY – вертикально вверх или вниз, как вам больше нравится. Запишите уравнения движения в проекциях на выбранные оси. Внимательно следите за правильным выбором знаков проекций, для этого обязательно в выбранной системе отсчета нарисуйте все векторы, определяющие движение. 
Решение и ответ
Задача 1.5. Снаряд, вылетевший из орудия под углом α к горизонту, находился в полете в течение времени Т = 12 с. Определите наибольшую высоту подъема снаряда. Сопротивлением воздуха можно пренебречь.

Указания (подсказка)
Выберите горизонтальную ось ОХ – вдоль нее движение равномерное с начальной скоростью ʋ0 cos а – и вертикальную ось OY – по ней движение равнопеременное с начальной скоростью ʋ0 sin а и ускорением ау = –g. Запишите уравнения движения по этим осям. Время движения определите из второго уравнения. Далее учтите, что без учета сопротивления воздуха время подъема равно времени падения и в два раза меньше всего времени движения. Из полученных уравнений выведите математическую связь заданного времени и искомой высоты.
Решение и ответ
Задача 1.6. Камень брошен вертикально вверх со скоростью ʋ0 = 15 м/с. Определите, через сколько времени он окажется на высоте H = 3 м. Определите потенциальную и полную энергию камня в этот момент времени. Масса камня m = 0,2 кг.

Указания (подсказка)
В этой задаче движение только вдоль одной оси – оси OY – движение равнопеременное с начальной скоростью и ускорением свободного падения.  В условии этой задачи есть неточность – не сказано, относительно какого нулевого уровня выбирается значение потенциальной энергии. Выбирайте сами! Правда, лучше выбрать уровень начала движения. Вспомните формулы для кинетической энергии (mʋ2/2) и потенциальной энергии в поле тяжести Земли (mgh, где h – расстояние от выбранного нулевого уровня).
Решение и ответ
Задача 1.7. Тело свободно падает с некоторой высоты H. Путь, пройденный им за последнюю секунду, в 7 раз больше пути, пройденного за первую секунду. Определите время падения и высоту Н.

Указания (подсказка)
Задачу можно решать, записывая уравнения свободного падения тел. Помните, что путь – это разность координат.  Можно задачу решить графически. Постройте график зависимости скорости от времени для свободного (равноускоренного) падения. Площадь под графиком определяет пройденный путь. Остается вспомнить математическую запись площади треугольника и площади трапеции. Сравните площади, следовательно, и пути за указанные в задаче интервалы времени.
Решение и ответ
Задача 1.8. В последнюю секунду свободного падения тело прошло путь, в 2 раза больший, чем в предыдущую. Определите время падения и высоту, с которой падало тело.

Указания (подсказка)
Воспользуйтесь указанием к задаче 1.7.
Решение и ответ
Задача 1.9. Два тела бросили вертикально вверх с одинаковой скоростью ʋ0 = 20 м/с через промежуток времени t = 1 с одно после другого. Определите, где и когда (через сколько времени после бросания первого тела) они встретятся. Примите g = 10 м/с2.

Указания (подсказка)
В этой задаче рассматривается движение двух тел, но вдоль одной и той же оси. Составьте уравнения для каждого тела, не забудьте, что одно из них до столкновения двигалось больше времени. Равенство координат – условие встречи тел. Можно рассматривать движение одного тела относительно другого.
Решение и ответ
Задача 1.10. Тело массой М = 1 кг бросают под углом α к горизонту. Определите этот угол, если известно, что кинетическая энергия тела в точке максимального подъема составляет 25% от его кинетической энергии в момент бросания, а потенциальная энергия относительно точки бросания Еп = 24 Дж. Определите дальность полета и максимальную высоту подъема этого тела.

Указания (подсказка)
Использование закона сохранения механической энергии позволит легко решить эту задачу. Начальная энергия – только кинетическая Eко = (mʋ0)2/2, полная механическая энергия в верхней точке траектории Е = Еп – Ек.
Решение и ответ

Вы смотрели «ЕГЭ Решение задач по физике. Механика 01-10». Задачи ЕГЭ по физике с указаниями, подсказками, ответами и решениями (ГДЗ по ЕГЭ). Материал для подготовки к ЕГЭ по физике.

Вернуться к Списку заданий тренинга по физике.

Читать далееЧитать далее