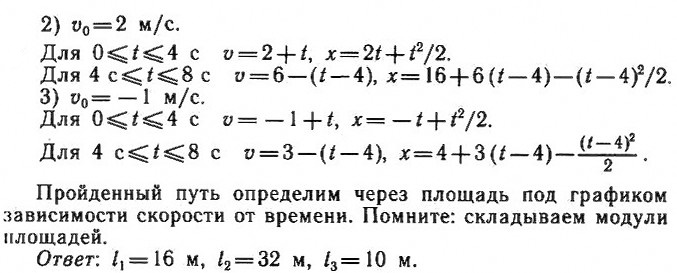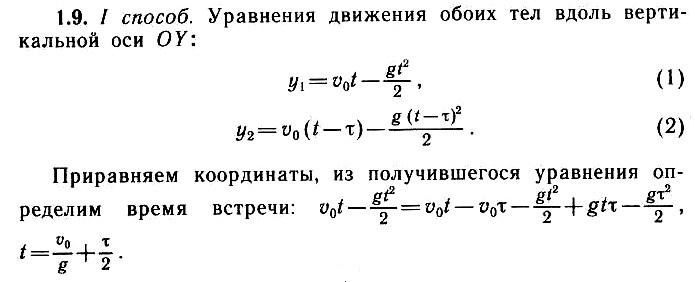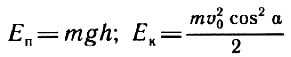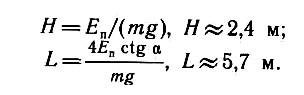ЕГЭ Решение задач по физике. Глава 1. МЕХАНИКА (кинематика, динамика, статика, колебания и волны). Задачи ЕГЭ по физике М01 — М10 с указаниями, подсказками, ответами и решениями (ГДЗ для ЕГЭ). Материал для подготовки к ЕГЭ по физике может быть использован репетиторами, учителями и самими учащимися.
Вернуться к Списку заданий тренинга по физике.
Задачи по физике. Механика 01-10
Задача 1.1. Движение материальной точки задано уравнением
x = At+ Bt2, где
А = 2 м/с,
В = –2 м/с2. Определите ускорение движения точки н путь, пройденный ею до остановки. Постройте графики зависимости от времени ускорения, скорости и координаты.
Указания (подсказка)
При решении этой задачи обычно возникают математические трудности. Вспомните, что скорость определяется как производная по времени от функции координаты, а ускорение – как производная по времени от функции скорости. Но вы забыли это определение или забыли, как надо взять производные. Что делать? Запишите основные два уравнения:
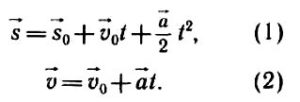
В момент времени, когда скорость равна нулю, s и есть пройденный путь.
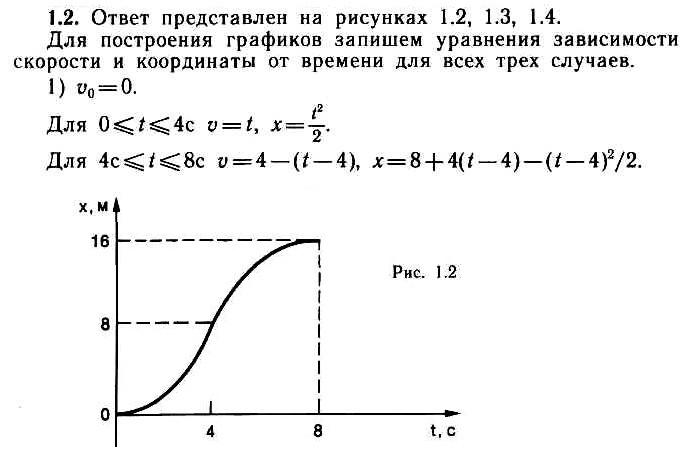
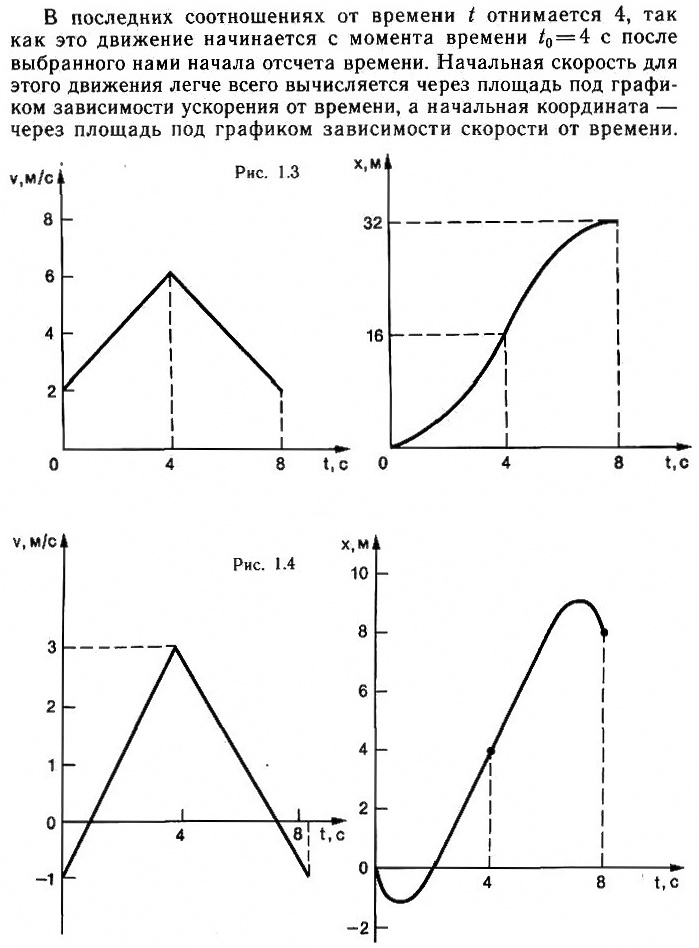
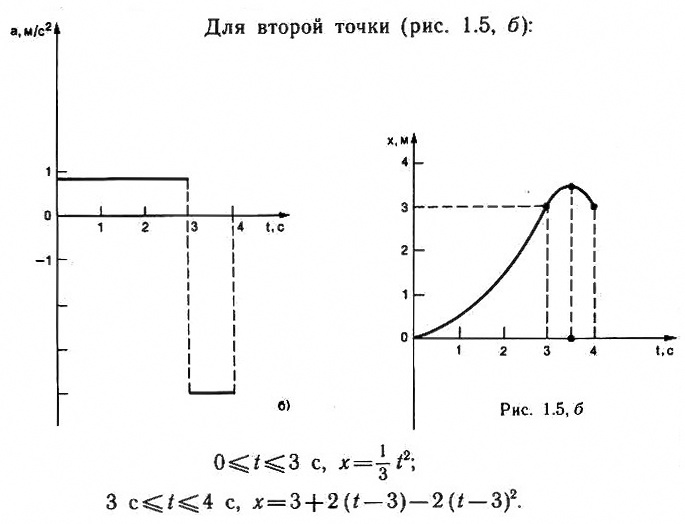
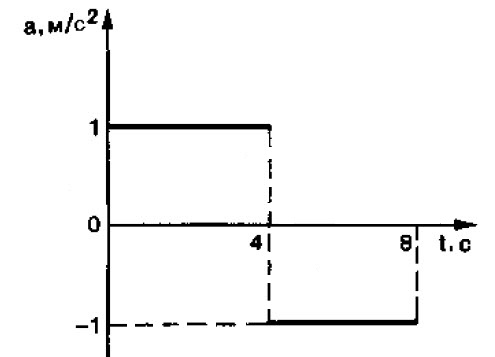
На рисунке дан график зависимости ускорения от времени при прямолинейном движении материальной точки. Постройте графики зависимости скорости от времени для этого движения. Определите путь, пройденный точкой за все время движения. Рассмотрите случаи, когда: 1) начальная скорость равна нулю; 2) начальная скорость
ʋ0 = 2 м/с; 3) начальная скорость
ʋ0 = – 1 м/с. Постройте также графики зависимости координаты от времени; начальная координата равна нулю (
х0 = 0).
задача 1.2
Указания (подсказка)
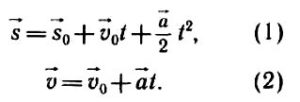
Внимательно изучите график. На промежутке 0 ≤ t ≤ 4 с ускорение постоянно и положительно; следовательно, его направление совпадает с направлением выбранной системы координат, площадь под графиком определяет приращение скорости. Для промежутка времени 4 с ≤ t ≤ 8 с движение равнозамедленное ускорение отрицательно. Составьте уравнения зависимости скорости и координаты от времени, руководствуясь соотношениями (1) и (2). Не забудьте при этом о выборе начала отсчета времени. Вспомните также, что путь определяется площадью под графиком зависимости скорости от времени; суммируйте все площади и над осью времени, и под осью времени.
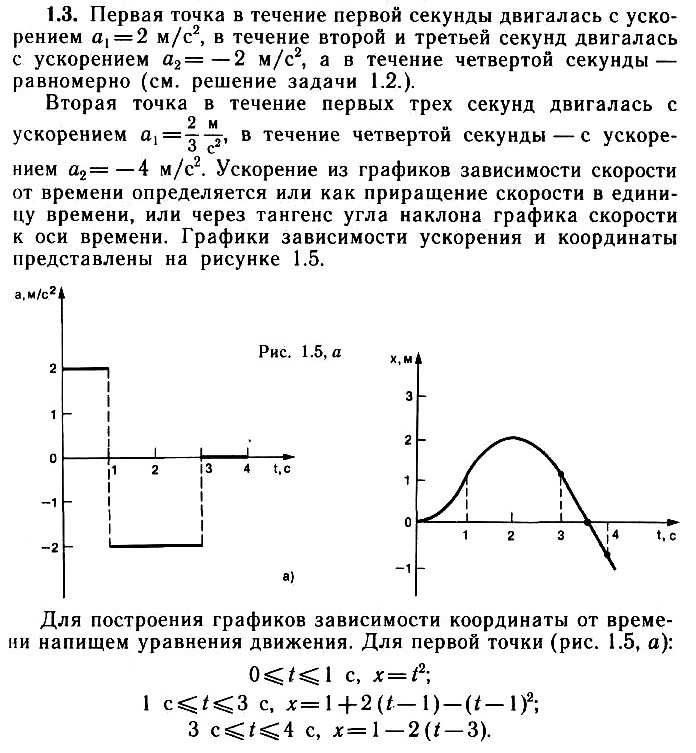
Две материальные точки движутся прямолинейно. Графики зависимости скорости от времени приведены на рисунке; ломаная ОАВС – для первой точки, ODC – для второй. Опишите характер движения точек. Постройте графики зависимости ускорения и координаты от времени.
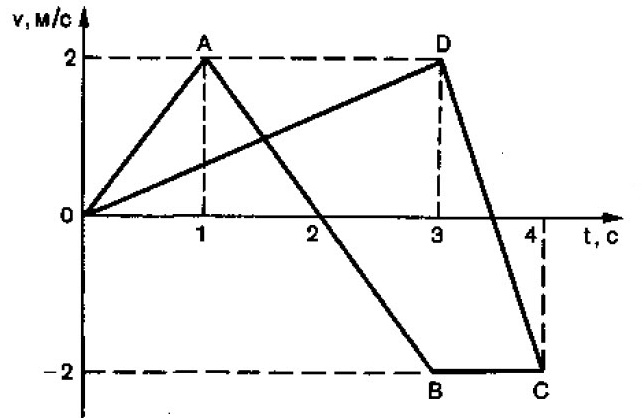
задача 1.3
Указания (подсказка)
Воспользуйтесь указанием к задаче 1.2.
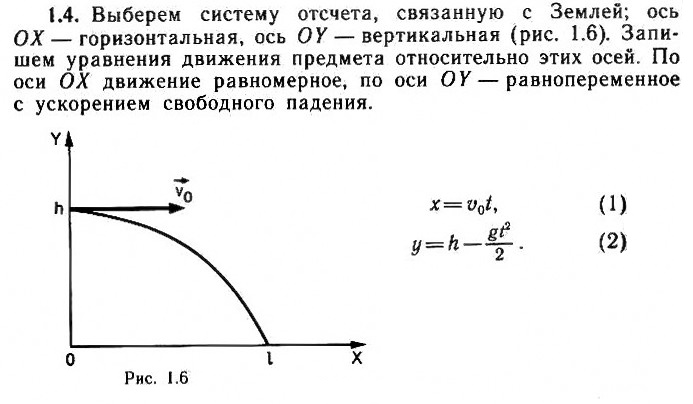
Из окна вагона, движущегося по горизонтальному пути со скоростью
ʋ = 54 км/ч, выпал предмет. Окно расположено на высоте
h = 2,5 м от поверхности земли. Определите расстояние от места, где предмет выпал из окна, до места его падения на землю.
Указания (подсказка)
Выберите систему координат, взяв за начало отсчета точку бросания; ось ОХ – горизонтально направленную вдоль движения вагона, ось OY – вертикально вверх или вниз, как вам больше нравится. Запишите уравнения движения в проекциях на выбранные оси. Внимательно следите за правильным выбором знаков проекций, для этого обязательно в выбранной системе отсчета нарисуйте все векторы, определяющие движение.
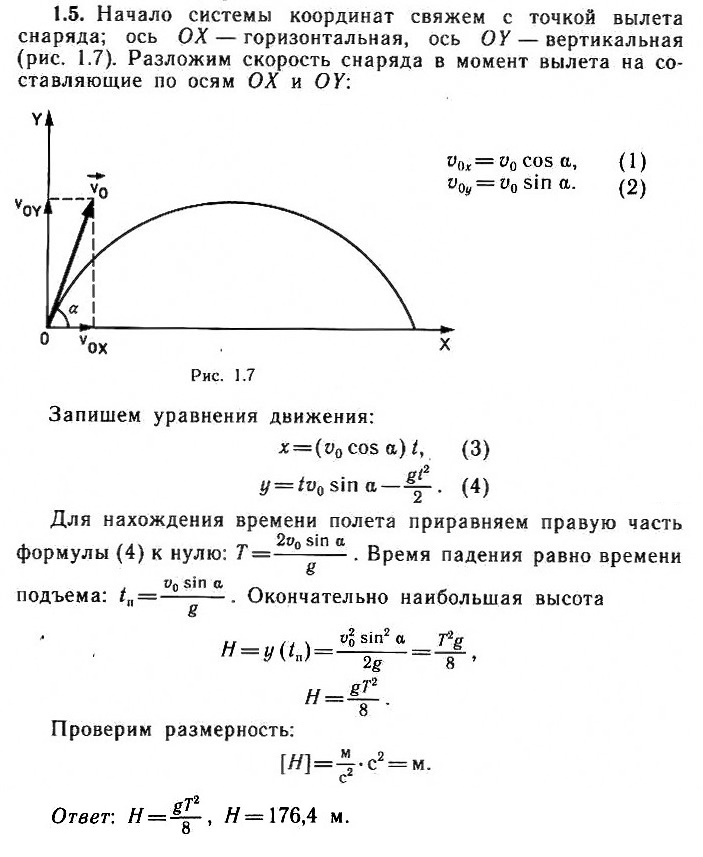
Снаряд, вылетевший из орудия под углом
α к горизонту, находился в полете в течение времени
Т = 12 с. Определите наибольшую высоту подъема снаряда. Сопротивлением воздуха можно пренебречь.
Указания (подсказка)
Выберите горизонтальную ось ОХ – вдоль нее движение равномерное с начальной скоростью ʋ0 cos а – и вертикальную ось OY – по ней движение равнопеременное с начальной скоростью ʋ0 sin а и ускорением ау = –g. Запишите уравнения движения по этим осям. Время движения определите из второго уравнения. Далее учтите, что без учета сопротивления воздуха время подъема равно времени падения и в два раза меньше всего времени движения. Из полученных уравнений выведите математическую связь заданного времени и искомой высоты.
Камень брошен вертикально вверх со скоростью
ʋ0 = 15 м/с. Определите, через сколько времени он окажется на высоте
H = 3 м. Определите потенциальную и полную энергию камня в этот момент времени. Масса камня
m = 0,2 кг.
Указания (подсказка)
В этой задаче движение только вдоль одной оси – оси OY – движение равнопеременное с начальной скоростью и ускорением свободного падения. В условии этой задачи есть неточность – не сказано, относительно какого нулевого уровня выбирается значение потенциальной энергии. Выбирайте сами! Правда, лучше выбрать уровень начала движения. Вспомните формулы для кинетической энергии (mʋ2/2) и потенциальной энергии в поле тяжести Земли (mgh, где h – расстояние от выбранного нулевого уровня).
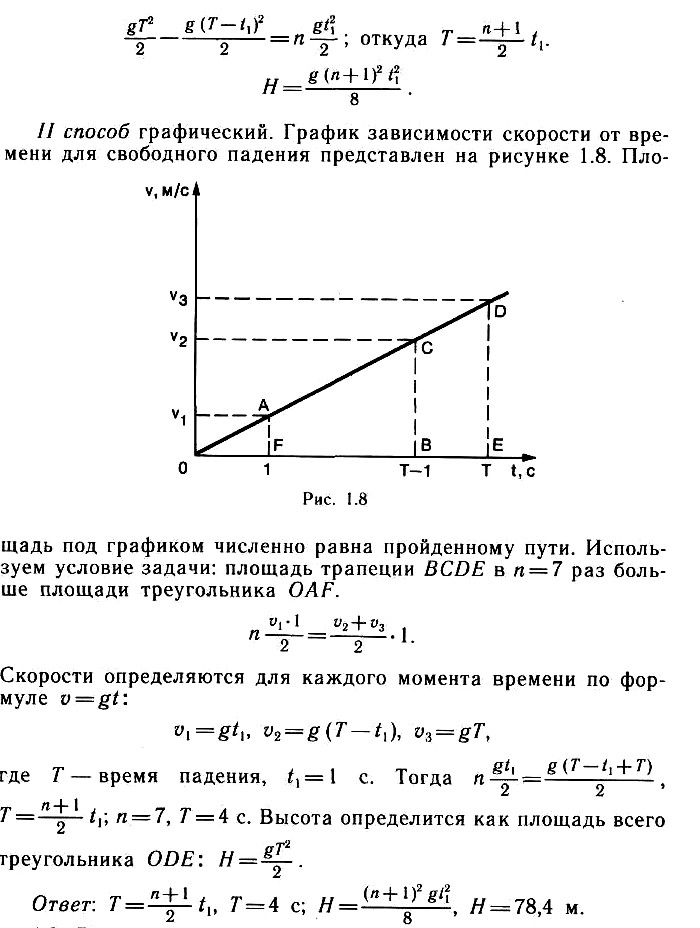
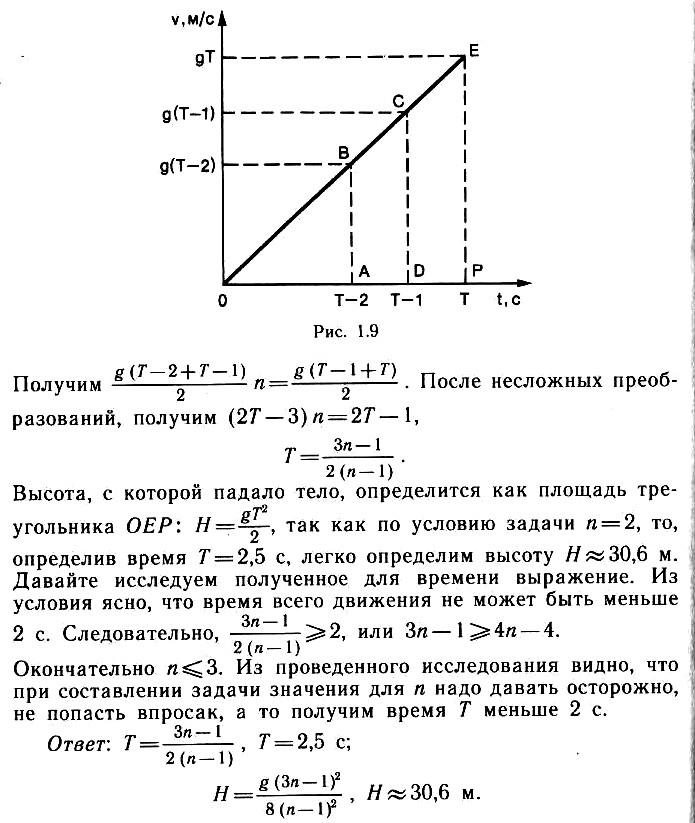
Тело свободно падает с некоторой высоты
H. Путь, пройденный им за последнюю секунду, в 7 раз больше пути, пройденного за первую секунду. Определите время падения и высоту
Н.
Указания (подсказка)
Задачу можно решать, записывая уравнения свободного падения тел. Помните, что путь – это разность координат. Можно задачу решить графически. Постройте график зависимости скорости от времени для свободного (равноускоренного) падения. Площадь под графиком определяет пройденный путь. Остается вспомнить математическую запись площади треугольника и площади трапеции. Сравните площади, следовательно, и пути за указанные в задаче интервалы времени.
В последнюю секунду свободного падения тело прошло путь, в 2 раза больший, чем в предыдущую. Определите время падения и высоту, с которой падало тело.
Указания (подсказка)
Воспользуйтесь указанием к задаче 1.7.
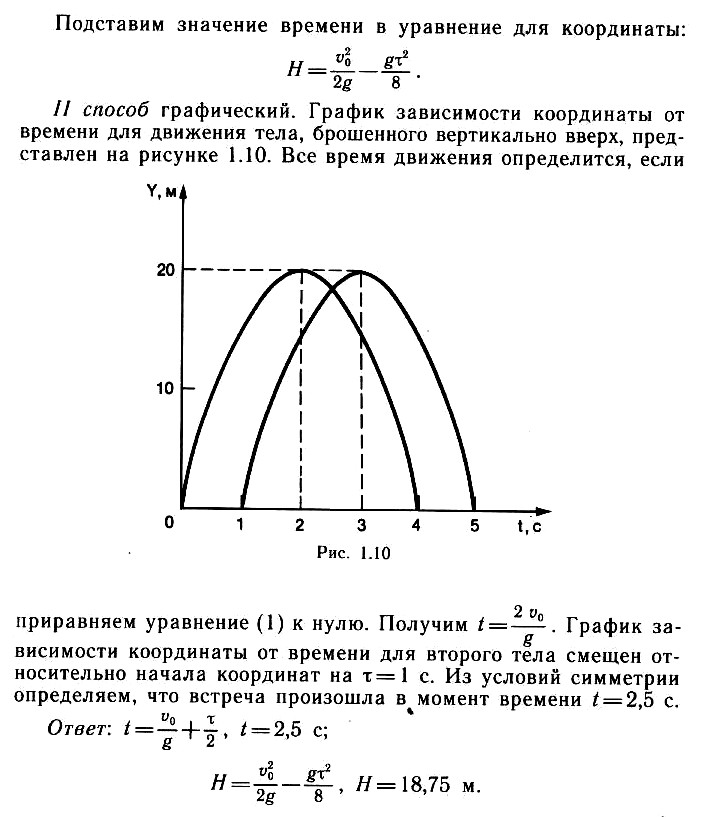
Два тела бросили вертикально вверх с одинаковой скоростью
ʋ0 = 20 м/с через промежуток времени
t = 1 с одно после другого. Определите, где и когда (через сколько времени после бросания первого тела) они встретятся. Примите
g = 10 м/с2.
Указания (подсказка)
В этой задаче рассматривается движение двух тел, но вдоль одной и той же оси. Составьте уравнения для каждого тела, не забудьте, что одно из них до столкновения двигалось больше времени. Равенство координат – условие встречи тел. Можно рассматривать движение одного тела относительно другого.
Тело массой
М = 1 кг бросают под углом
α к горизонту. Определите этот угол, если известно, что кинетическая энергия тела в точке максимального подъема составляет 25% от его кинетической энергии в момент бросания, а потенциальная энергия относительно точки бросания
Еп = 24 Дж. Определите дальность полета и максимальную высоту подъема этого тела.
Указания (подсказка)
Использование закона сохранения механической энергии позволит легко решить эту задачу. Начальная энергия – только кинетическая E
ко = (mʋ
0)
2/2, полная механическая энергия в верхней точке траектории Е = Еп – Ек.
Вы смотрели «ЕГЭ Решение задач по физике. Механика 01-10». Задачи ЕГЭ по физике с указаниями, подсказками, ответами и решениями (ГДЗ по ЕГЭ). Материал для подготовки к ЕГЭ по физике.
Вернуться к Списку заданий тренинга по физике.


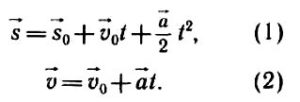 В момент времени, когда скорость равна нулю, s и есть пройденный путь.
В момент времени, когда скорость равна нулю, s и есть пройденный путь.