Материалы для подготовки к ЕГЭ. Справочник по математике.
Раздел 2 «Выражения» (параграфы 5 — 10). Целые рациональные, дробные рациональные, иррациональные выражения. Преобразование выражений, содержащих переменную под знаком логарифма. Формулы тригонометрии и их использование для преобразования тригонометрических выражений
Раздел II. Выражения
Содержание страницы
Раздел II. Выражения
§ 5. Основные понятия.
51. Виды алгебраических выражений.

52. Допустимые значения переменных. Область определения алгебраического выражения.

53. Понятие тождественного преобразования выражения. Тождество.


§ 6. Целые рациональные выражения.
54. Одночлены и операции над ними.


55. Многочлены. Приведение многочленов к стандартному виду.


56. Формулы сокращенного умножения.

57. Разложение многочленов на множители.



58. Многочлены от одной переменной.

59. Деление многочленов. Схема Горнера. Теорема Безу.




60. Разложение квадратного трехчлена на линейные множители.

61. Разложение на множители двучлена хn — аn.
62. Возведение двучлена в натуральную степень (формула бинома Ньютона).


§ 7. Дробные рациональные выражения.
63. Рациональная дробь и ее основное свойство.


64. Сокращение рациональных дробей.

65. Приведение рациональных дробей к общему знаменателю.


66. Сложение и вычитание рациональных дробей.


67. Умножение и деление рациональных дробей.


68. Возведение рациональной дроби в целую степень.

69. Преобразование рациональных выражений.


§ 8. Иррациональные выражения.
70. Простейшие преобразования арифметических корней (радикалов).


71. Тождество √а2 = |а|.

72. Преобразование иррациональных выражений.
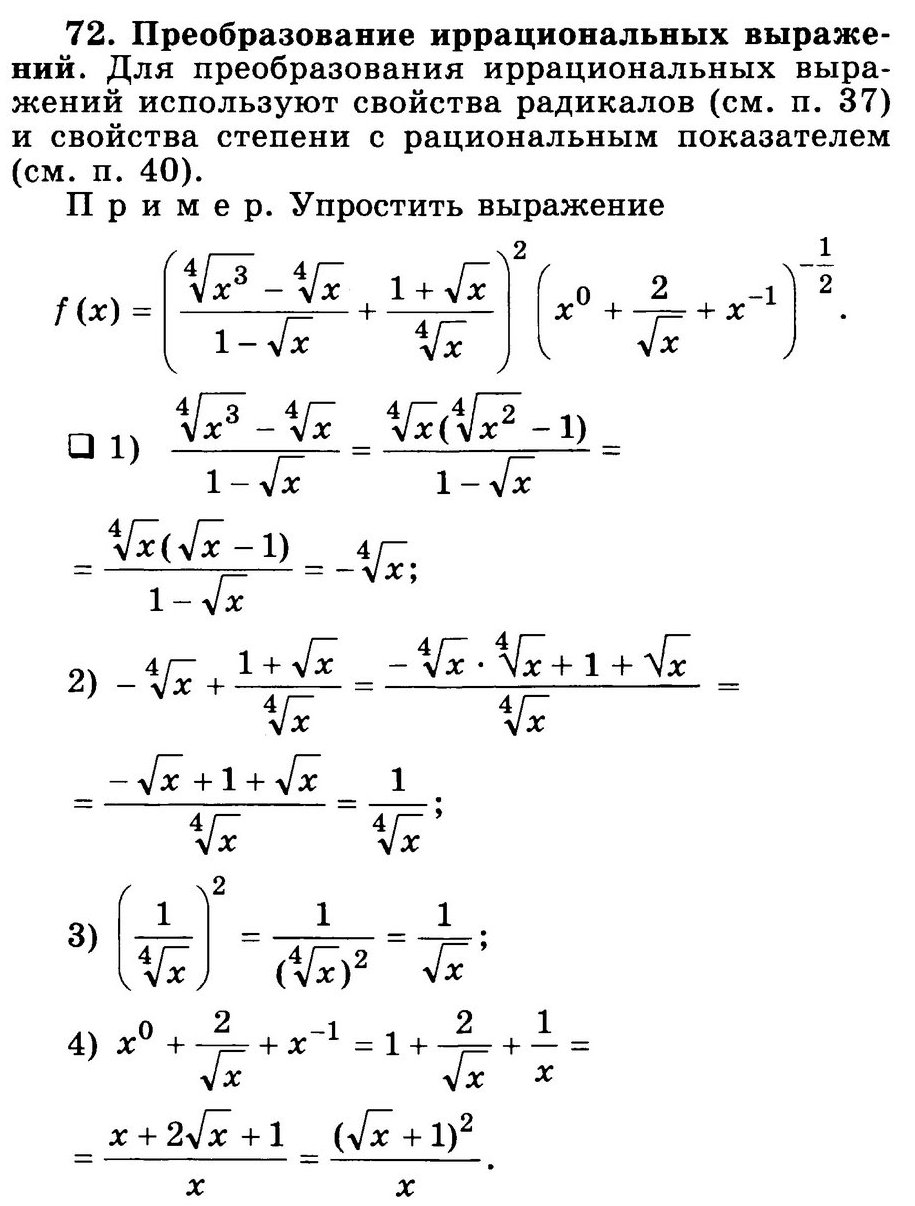

§ 9. Преобразование выражений, содержащих переменную под знаком логарифма.
73. Понятие трансцендентного выражения.

74. Определение логарифма положительного числа по данному основанию.
75. Свойства логарифмов.


76. Логарифмирование и потенцирование.


77. Десятичный логарифм. Характеристика и мантисса десятичного логарифма.


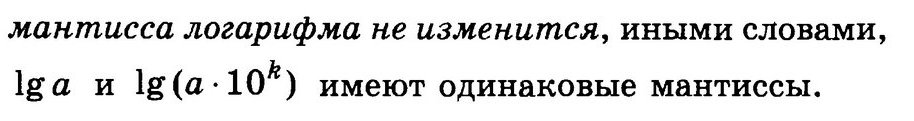
§10. Формулы тригонометрии и их использование для преобразования тригонометрических выражений.
78. Тригонометрические выражения.
79. Формулы сложения и вычитания аргументов.


80. Формулы приведения.

81. Соотношения между тригонометрическими функциями одного и того же аргумента.


82. Формулы двойного угла.

83. Формулы понижения степени.


84. Выражение sin t, cos t и tg t через tg t/2

85. Преобразование суммы тригонометрических функций в произведение.


86. Преобразование произведения тригонометрических функций в сумму.

87. Преобразование выражения a cos t + b sin t к виду A sin (t + α).


88. Преобразование выражений, содержащих обратные тригонометрические функции.


Материалы для подготовки к ЕГЭ. Справочник по математике. Раздел 2 «Выражения». Целые рациональные, дробные рациональные, иррациональные выражения. Преобразование выражений, содержащих переменную под знаком логарифма. Формулы тригонометрии и их использование для преобразования тригонометрических выражений.